Subspace-Configurable Networks

 

 

Tips

Follow the links to visualize β-space for the selected setting. Double-click on a label in the legend to hide all other βi.

Interactive 3D surfaces can aid visual understanding.

Visualization of nicely shaped β space of 3D rotation

In this section, we take Subspace Configurable LeNet-5 on 3D rotation as an example. The following pictures show the (β−α) space of this SCN's hyper-output.

 

ItemExplaination
βThe output of hypernet of a SCN
αiThe transformation parameters. Euler angles (α1,α2,α3) is the parameters for 3D rotations.
DThe dimensions of hyper-output, as well as the number of inference model.

 

 

β−α1,2

 

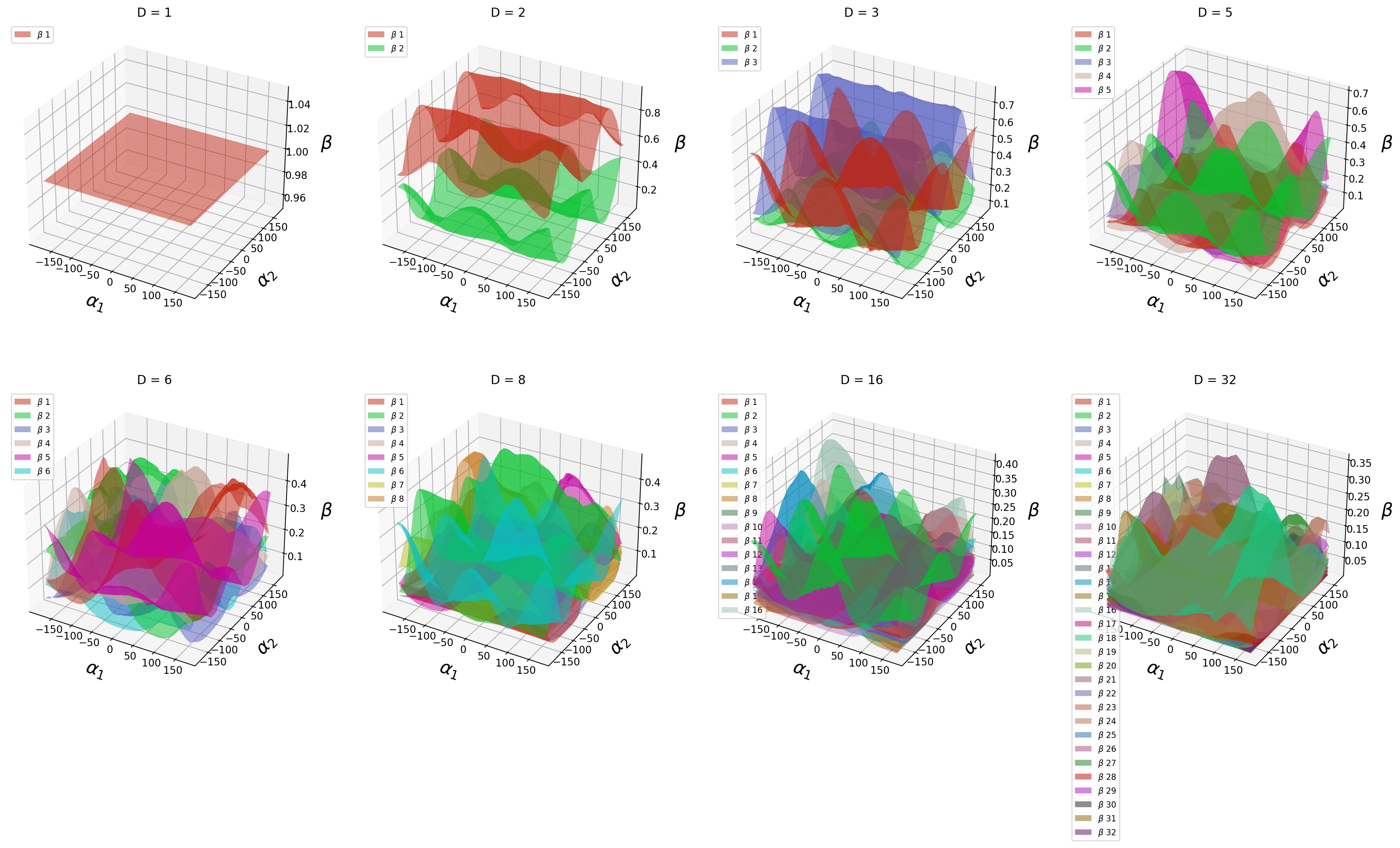
beta_alpha12

The following links to interactive webpages show the β−α1,2 space.

 

Links for 3D surfaceD=1D=2D=3D=5D=6D=8D=16D=32
Links for 3D pointsD=1D=2D=3D=5D=6D=8D=16D=32

 

 

β−α1,3

 

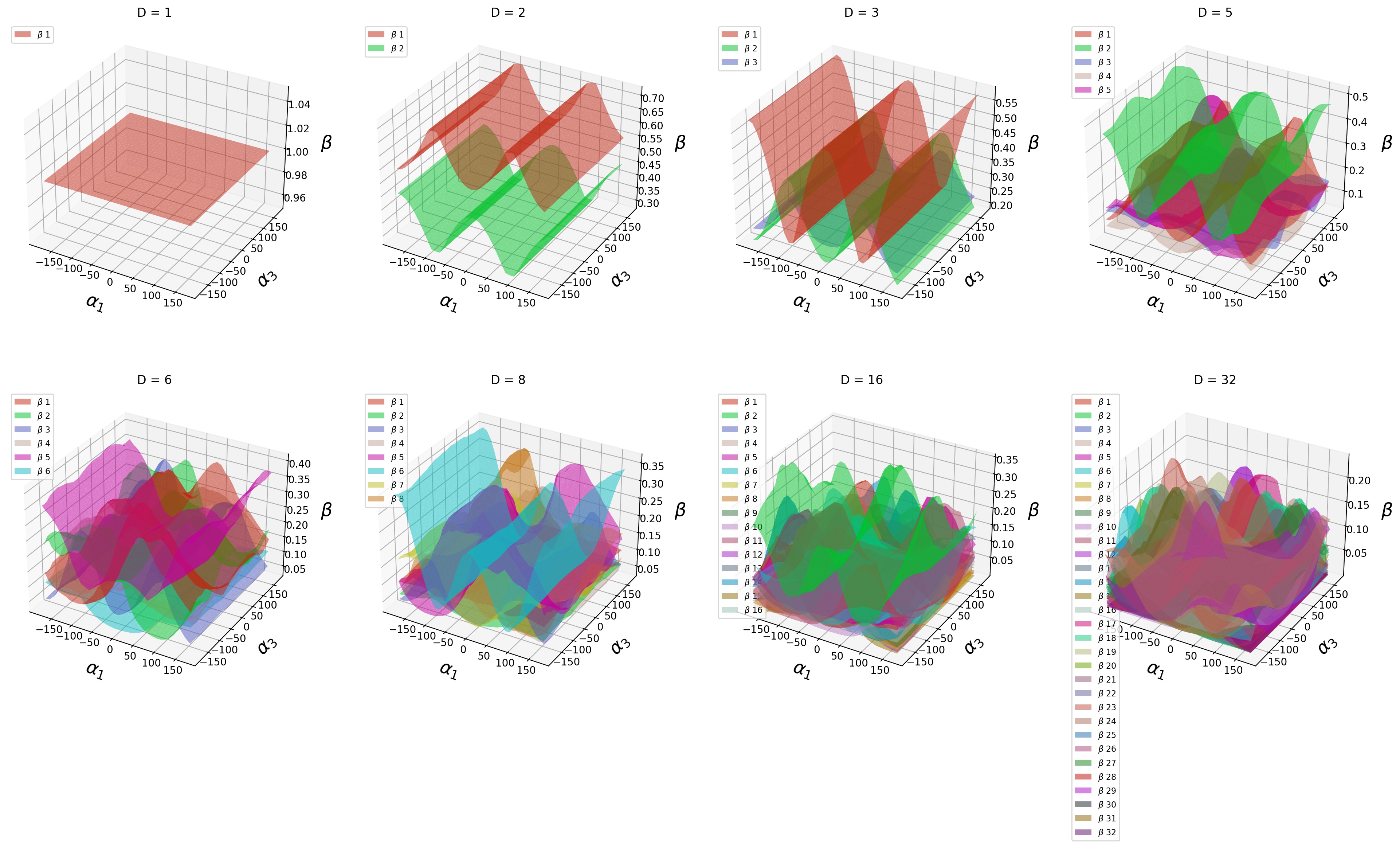
beta_alpha13

 

The following links to interactive webpages show the β−α1,3 space.

 

Links for 3D surfaceD=1D=2D=3D=5D=6D=8D=16D=32
Links for 3D pointsD=1D=2D=3D=5D=6D=8D=16D=32

 

 

β−α2,3

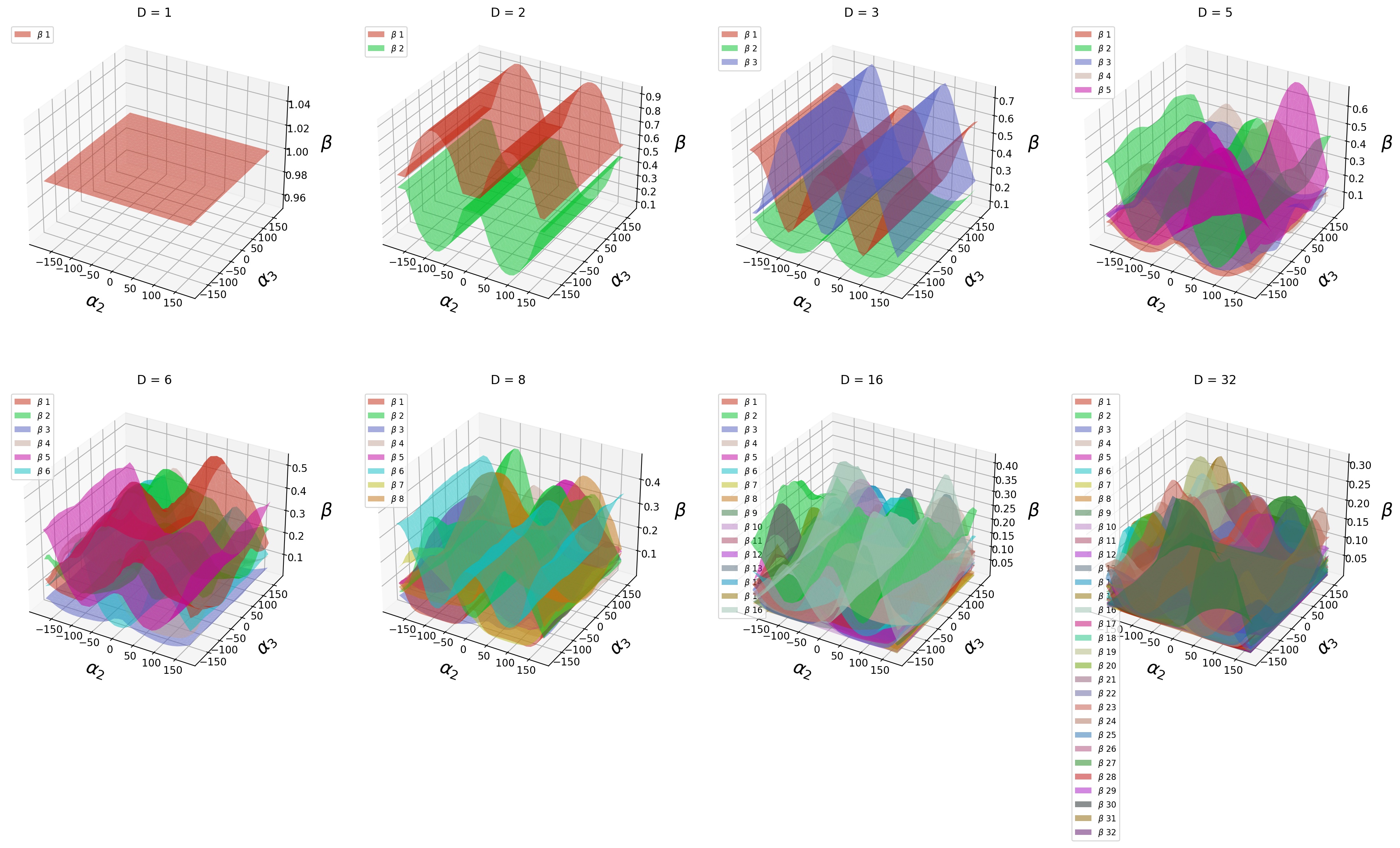
beta_alpha23

The following links to interactive webpages show the β−α2,3 space.

 

Links for 3D surfaceD=1D=2D=3D=5D=6D=8D=16D=32
Links for 3D pointsD=1D=2D=3D=5D=6D=8D=16D=32

 

 

 

 

Visualization of nicely shaped β space of 2D rotation

This section, we take Subspace Configurable MLP on 2D rotation as an example. The following pictures show the (β−α) space of this SCN's hyper-output.

 

ItemExplaination
βThe output of hypernet of a SCN
αThe transformation parameters. α vector (cos⁡(α)sin⁡(α)) is the parameters for 2D rotations.
DThe dimensions of hyper-output, as well as the number of inference model.

 

β−α

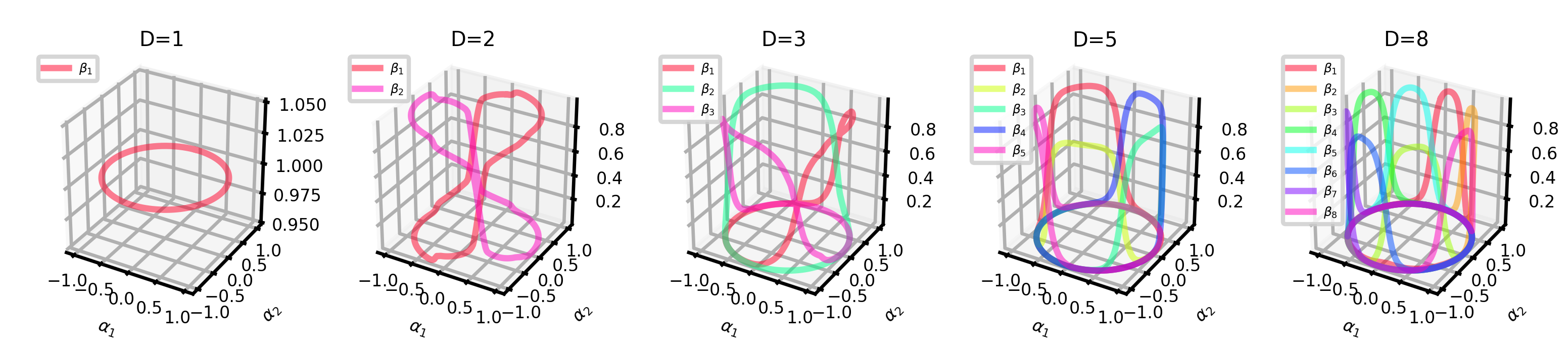
beta_alpha_2d_mlpb_fashionmnist

The following links to interactive webpages show the β−α space.

 

Links for 3D linesD=1D=2D=3D=5D=8